Загадки с подвохом для детей — самые интересные

Что такое загадки с подвохом, в чем их польза?

Логические загадки не имеют скучных ответов. Такие задачки в игровой форме тренируют воображение, учат обращать внимание на детали, рассуждать. Загадки с подвохом с ответами смешные и необычные, способны поставить в тупик человека любого возраста, а предельная простота ответа вызывает невольную улыбку. Правильное решение часто ставит представление о мире с ног на голову. Благодаря этому задачки расширяют кругозор, учат мыслить нелинейно. Они демонстрируют, что на самый сложный вопрос может существовать ответ, невидимый большинству людей из-за невероятной очевидности. Благодаря смешным логическим задачкам мозг интенсивно развивается.

Порой отгадка может занять немало времени даже у взрослого, поэтому выбирайте загадки с подвохом с ответами. Даже если никто из присутствующих не сумеет найти правильное решение, его всегда можно подсмотреть. От этого эффект не становится хуже! Ведь узнав необычный ответ, мы все равно начинаем иначе смотреть на окружающий мир.

Сложные загадки с подвохом подключают к поиску решения оба полушария мозга: нужно предугадать неоднозначность задачки, проанализировать всю полученную информацию, выявить возможные несоответствия, соотнести возможные ответы с реальностью. В результате на любые другие вопросы, жизненные вызовы дети начинают отвечать более творчески. Регулярные игровые тренировки даже помогают повысить успеваемость в школе.

Каждая загадка с подвохом с ответами для детей стимулирует фантазию – вскоре вся семья может увлечься сочинением аналогичных задачек.

Загадки с подвохом для детей можно использовать для развлечения всей семьей на отдыхе, в пути, на празднике. Такая развлекательная программа обязательно понравится ребятам школьного возраста. Собираетесь использовать задачки на логику в рамках утренника или семейного праздника? Ввести их в программу можно несколькими способами.

• Заполнение пауз. Задавайте смешные загадки с подвохом в промежутках между конкурсами, танцами, играми. Это станет прекрасным вариантом активности для маленьких и взрослых гостей.
• Индивидуальная викторина. Пусть игроки за каждый правильный ответ получают полоски цветной бумаги или игровые деньги. Победителей награждают сувенирами, сладостями либо шуточными медалями.
• Групповое соревнование. Чтобы призы получил каждый, объедините участников праздника в несколько команд и, используя загадки на логику с подвохом, устройте аналог «Что? Где? Когда?». Победители получат главный приз, проигравшие – утешительные подарки.

Независимо от выбранного формата развлечений, логические задачки для детей подарят массу позитивных эмоций, привьют любовь к обучению, сделают даже самое скучное времяпрепровождение увлекательным приключением.

Сколько горошин войдет в один стакан?

Сколько горошин войдет в один стакан? Наверняка вас хотя бы раз пытались подловить на этом вопросе. Что ж, благодаря игре слов, правильный ответ – ни одной, ведь горошины не умеют ходить, не так ли? А для тех, кто предпочитает избегать таких ловушек, существуют строгие условия математических задач. При этом вопрос будет точно такой же!

Для определенности возьмем ограниченное число небольших горошин – допустим, N. Горошины оказались рассыпаны по столу так, что любые три из них можно накрыть перевернутым стаканом – они окажутся внутри. Итак, обещанный вопрос: какое максимальное число горошин за раз можно накрыть стаканом? Давайте исследуем знаменитый вопрос шутников с математической точки зрения!

Прежде всего, договоримся считать небольшие горошины точками, а радиус стакана примем за единицу. Теперь условие выглядит совсем как из учебника по геометрии: на плоскости дано N точек, причем любые 3 из них можно накрыть кругом радиуса 1. Сколько точек может оказаться в таком круге? Пожалуй, начнем наше исследование с круга побольше, в котором поместятся все N точек на плоскости. Попробуем его уменьшить – и будем уменьшать до тех пор, пока это возможно. Обозначим радиус этого круга R. Так как полученный круг – минимальный для нашего набора точек, то по крайней мере две из них окажутся на его границе. Рассмотрим ситуацию, когда таких точек ровно две:

В этом случае точки окажутся диаметрально противоположными. Для того, чтобы проверить условие задачи, выберем третью точку – любую из оставшихся. Так как расстояние между первыми двумя точками равно длине диаметра – 2R, то и диаметр окружности с единичным радиусом, в которую должны попасть по условию все три выбранные точки, не может быть меньше. Получим 2 ≥ 2R, а это значит, что радиус минимального для нашего набора точек круга не превышает 1! В этом случае стаканом можно накрыть все N горошин на столе – причем N может быть любым.

Тем не менее, не стоит забывать – мы рассмотрели только один случай. Допустим теперь, что на границе оказалось ровно три точки – обозначим их А, В и С:

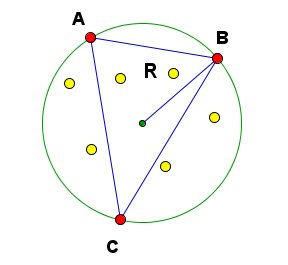
Задумайтесь: если бы треугольник АВС был тупоугольным, то радиус минимального круга для всего набора точек можно было бы уменьшить – по крайней мере, до тех пор, пока на границе не окажется еще одна точка. Если треугольник АВС оказался прямоугольным, то его гипотенуза будет диаметром нашего круга, а такую ситуацию мы уже рассмотрели для двух точек. Остается только тот вариант, при котором треугольник АВС – остроугольный, а значит, радиус его описанной окружности R не может быть больше 1, иначе не существовало бы единичной окружности, содержащий все три вершины А, В и С. Что ж, и в этом случае мы получили, что накрыть стаканом удастся сразу все горошины на столе!

Итак, нерассмотренным остался тот случай, при котором на границе общего круга окажется сразу четыре или больше точек. В таком случае, эти k точек делят окружность на k дуг а1 … ak:

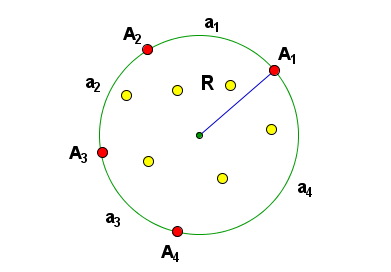
Так как точек больше трех, то мы пока не можем использовать условие задачи так же, как для предыдущих рассмотренный случаев. Значит, нужно уменьшить количество точек на окружности! Будем последовательно убирать те точки, сумма соседних дуг которых не превышает 180˚. Докажем, что, пока k ≥ 4, такие дуги найдутся: пусть а1 + а2 > 180˚, а2 + а3 > 180˚, … аk + а1 > 180˚. Сложим эти неравенства: 2(а1 + а2 +…+ аk) > k*180˚. Но ведь в сумме все эти дуги представляют собой полную окружность, то есть 360˚! Получаем, что для k ≥ 4 итоговое неравенство неверно, и в силу этого противоречия, соседние дуги с суммой не больше 180˚ будут находиться до тех пор, пока на границе круга не останется только 3 точки – а ведь такой случай мы с вами уже рассмотрели! Получается, что все точки, кроме удаленных нами с окружности, и в этот раз можно накрыть стаканом. При этом из-за того, что в стакан попадет вся итоговая окружность – ведь внутри окажется остроугольный треугольник, вокруг которого она описана – даже удаленные точки будут накрыты стаканом.

Подведем итоги: если каждые три из N горошин на столе можно накрыть стаканом, то все эти горошины войдут в стакан за один раз. Впрочем, на самом деле наше решение задачи не единственное. Для тех, кто любит решать задачи красиво – буквально одной теоремой! – зададим новую планку: подумайте, каким образом можно трактовать условие, чтобы ответить на вопрос можно было одним применением теоремы Хелли!

Другие загадки с подвохом

Что можно приготовить, но нельзя съесть?

Ответ: Домашнее задание

Можно ли зажечь спичку под водой?

Ответ: Если ты в подводной лодке, то да.

Два гвоздя упали в воду. Как фамилия грузина?

Ответ: Заржавели.

Что в России на первом месте, а во Франции на втором?

Ответ: Буква Р.

Без работы висит, при работе стоит, после работы – мокрый.

Ответ: Зонт.

Сколько горошин может войти в один стакан?

Ответ: Нисколько, потому что горошины не ходят сами.

Какой рукой лучше всего размешивать чай?

Ответ: В которой ложка.

Что бросают, когда нуждаются в этом, и поднимают, когда в этом нет нужды?

Ответ: Якорь.

Что станет с зеленым утесом, если он упадет в Красное море?

Ответ: Раскрошится немного.

Какое слово всегда звучит неверно?

Ответ: Слово «неверно».